
- מְחַבֵּר Lynn Donovan [email protected].
- Public 2023-12-15 23:47.
- שונה לאחרונה 2025-01-22 17:25.
מיון ערימה הוא אלגוריתם במקום. מורכבות זמן : מורכבות הזמן של heapify הוא O(Logn). מורכבות הזמן של createAndBuildHeap() הוא O(n) ובסך הכל מורכבות הזמן מיון ערימה הוא O(nLogn).
לגבי זה, מהו האלגוריתם לסוג ערימה?
אלגוריתם מיון ערימה מחולק לשני חלקים בסיסיים: יצירת א ערימה של הרשימה/המערך הלא ממוין. ואז א מְמוּיָן מערך נוצר על ידי הסרה חוזרת ונשנית של האלמנט הגדול/הקטן ביותר מה- ערימה , והכנסתו למערך. ה ערימה נבנה מחדש לאחר כל הסרה.
באופן דומה, מהו זמן הריצה הטיפוסי של אלגוריתם מיון ערימה? עם זאת, למיון מהיר יש את המקרה הגרוע ביותר זמן ריצה של O (n 2) O(n^2) O(n2) ומורכבות רווח במקרה הגרוע ביותר של O (log ? n O(log n O(logn), אז אם זה מאוד חשוב שיהיה המקרה הגרוע המהיר ביותר זמן ריצה ושימוש יעיל במקום, מיון ערמות היא האפשרות הטובה ביותר.
באופן דומה, נשאל, מהי המורכבות של פונקציית Heapify?
הרעיון המרכזי הוא שב-build_heap אַלגוֹרִיתְם בפועל להגביר העלות אינה O(log n) עבור כל האלמנטים. כאשר להגביר נקרא, זמן הריצה תלוי באופן שבו אלמנט Faran עשוי לנוע למטה בעץ לפני שהתהליך מסתיים. במילים אחרות, זה תלוי בגובה האלמנט בערימה.
לאיזה אלגוריתם מיון יש את המורכבות האסימפטוטית הטובה ביותר?
ל הטוב ביותר הכנסת מקרה סוג ו-Heap מיון הם הטובים ביותר אחד כמוהם הטוב ביותר זמן ריצת מקרה מוּרכָּבוּת הוא O(n). למקרה ממוצע האסימפטוטי הטוב ביותר זמן ריצה מוּרכָּבוּת הוא O(nlogn) אשר ניתן על ידי מיזוג סוג , ערימה סוג , מהיר סוג . למקרה הגרוע ביותר הטוב ביותר זמן ריצה מוּרכָּבוּת הוא O(nlogn) אשר ניתן על ידי מיזוג סוג , ערימה סוג.
מוּמלָץ:
לאיזה אלגוריתם מיון יש את המורכבות האסימפטוטית הטובה ביותר?

מיון ערימה
איזה אלגוריתם מיון הוא הטוב ביותר במקרה הגרוע?
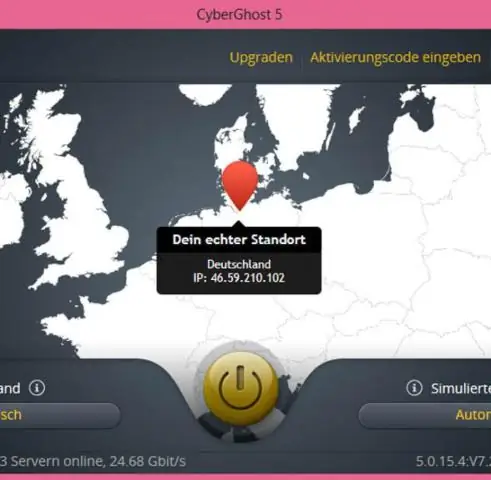
מיון אלגוריתמים אלגוריתם מבנה נתונים מורכבות זמן: הגרוע ביותר מיון מהיר מערך O(n2) מיזוג מיון מערך O(n log(n)) מיון ערימה מערך O(n log(n)) מיון חלק מערך O(n log(n))
מהי המורכבות של האלגוריתם של דיקסטרה?

מורכבות הזמן של האלגוריתם של דיקסטרה היא O (V 2) אך עם תור עדיפות מינימלית הוא יורד ל-O (V + E l o g V)
למה משמש מיון ערימה?
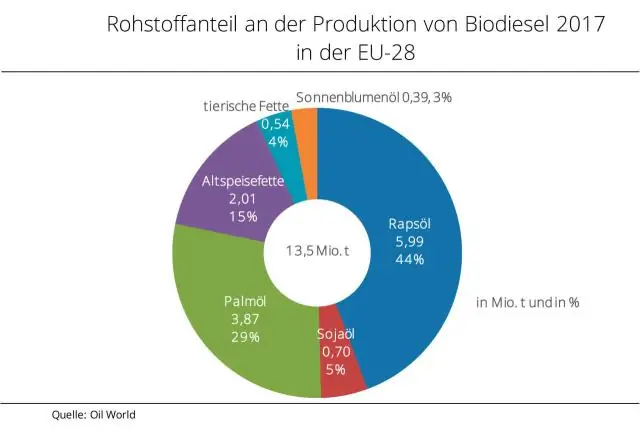
אלגוריתם מיון הערמות נמצא בשימוש נרחב בגלל היעילות שלו. מיון ערימה פועל על ידי הפיכת רשימת הפריטים שיש למיין למבנה נתונים ערימה, עץ בינארי עם מאפייני ערימה. בעץ בינארי, לכל צומת יש, לכל היותר, שני צאצאים
האם אלגוריתם מיון הדלי קיים?

לא, זה לא אלגוריתם מיון במקום. כל הרעיון הוא שהקלט ממיין את עצמו כשהם מועברים לדליים. במקרים הגרועים שבמקרים הטובים (ערכים עוקבים, אך ללא חזרה) השטח הנוסף הדרוש הוא גדול כמו המערך המקורי
